Praca z Excelem – 100 porad i tricków (4/5)
W czwartej odsłonie będziemy kontynuować rozpoczęty w poprzedniej odsłonie wątek. Będzie wiec dalej o formułach, ale tym razem z innych grup – przejdziemy do formuł statystycznych i finansowych. Nie ukrywam, że najbliższe moim zainteresowaniem i doświadczeniu zawodowemu, są formuły z tej ostatniej grupy – dlatego też to właśnie o nich będzie najwięcej. Mam nadzieję, że okażą się one dla Was przydatne, np. do uzupełniania o dodatkowe informacje budżetu domowego. Formuły statystyczne i matematyczne omówię w zakresie, który wykorzystuję do przetwarzania danych na potrzeby innych zastosowań. Jeżeli jednak liczycie na zaawansowany poradnik analizy statystycznej, to być może będziecie nieco zawiedzeni. Z przydatniejszych rzeczy pokażemy sobie też działanie jednego z częściej wykorzystywanych dodatków do Excela – Analysis Toolpak.
Zachęcam do zapoznania się z poprzednimi artykułami z cyklu:
Praca z Excelem – 100 porad i tricków (1/5)
Praca z Excelem – 100 porad i tricków (2/5)Praca z Excelem – 100 porad i tricków (3/5) #61 Pracujemy na szeregach liczb – wartości minimalne, maksymalne, średnie i inne podstawowe formuły
Zacznijmy od czegoś na rozgrzewkę. Excel pozwala na przetwarzanie pokaźnych ilości danych. Czasem przydatne może być jednak wyłuskanie jedynie pojedynczych kwot granicznych – maksymalnych lub minimalnych. Jeżeli nie chcemy w tym celu korzystać z szeregowania wartości, możemy posłużyć się prostymi formułami:
=MIN(zakres)
lub
=MAX(zakres)
Korzystanie z nich nie powinno przysporzyć żadnego problemu – nawet jeżeli nie mieliście zbyt wiele styczności z Excelem, to z pewnością po przeczytaniu ostatnich artykułów z naszego cyklu, potraficie się już poruszać w tym programie 😉
Excel umożliwia też wyliczenia różnego rodzaju średnich – warunkowych (średnia z wartości spełniających dane kryteria), arytmetycznych, geometrycznych, harmonicznych.
Najbardziej typową średnią będzie arytmetyczna, dana formułą:
=ŚREDNIA(zakres)
Jest jednak pewna odmiana tej funkcji, określana jako:
=ŚREDNIA.A
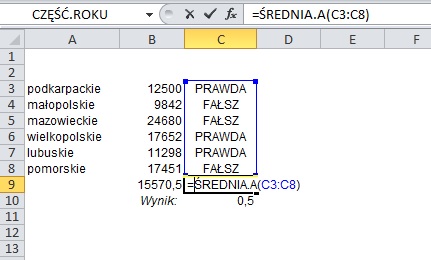
Dopisek „.A” pozwala na wyciąganie wartości z danych tekstowych, dla których wartościom PRAWDA przypisywana jest jedynka, a FAŁSZ (i innym dopiskom tekstowym) – zero. Jest to przydatne, gdy, korzystając np. z funkcji JEŻELI, chcemy szybko zweryfikować, jaki procent pozycji spełnia danych warunek (posiada dopisek PRAWDA).
O średniej ŚREDNIA.JEŻELI pisaliśmy w poprzednim artykule – liczy ona średnią arytmetyczną, w oparciu o założony warunek. ŚREDNIA.WARUNKÓW może spełniać więcej niż jeden warunek.
Przejdźmy jeszcze pokrótce przez podstawowe formuły statystyczne Excela.
=MEDIANA – inaczej drugi kwartyl, inaczej – wartość środkowa, poniżej i powyżej której znajduje się tyle samo obserwacji (lub jest to średnia z dwóch środkowych obserwacji). Różnicę między medianą a średnia najlepiej można pokazać na przykładzie statystyki wynagrodzeń. Nasz rzetelny GUS publikuje jednak dane odnośnie mediany raz na dwa lata, ale z danych z roku 2012 wynika, że średnia płaca wynosiła wówczas 3895,72 zł, podczas gdy mediana 3115,11 zł.
=WYST.NAJCZĘŚCIEJ – jest to po prostu dominanta, czyli wartość najczęściej występująca w zbiorze. (W 2012 r. takie wynagrodzenie wynosiło 2189,11 zł.)
=ODCH.STANDARDOWE; =WARIANCJA – Wikipedia podpowiada, że przytoczone dwie formuły, należą w statystyce, po średniej arytmetycznej, do najbardziej podstawowych miar statystycznych. I rzeczywiście. Są to miary zmienności, które określają rozproszenie danych wokół średniej arytmetycznej. Im wartość jest większa, tym dane bardziej się różnią. Odchylenie standardowe uzyskuje się jako pierwiastek kwadratowy z wariancji, która z kolei jako miara statystyczna nie ma sensownej interpretacji, gdyż wynik stanowi wartość podniesioną do kwadratu (np. wariancji wynosi 120 zł^2).
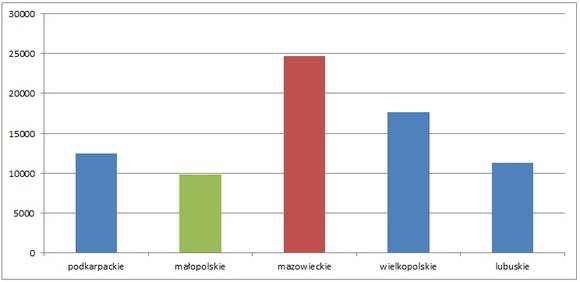
#62 Jak pokazać wartości minimalne i maksymalne na wykresie?
Przy okazji tego krótkiego wstępu, przypomniało mi się jeszcze jedno zastosowanie funkcji MAX i MIN. Są one nad wyraz przydatne, gdy wartości minimalne i maksymalne chcielibyśmy pokazać na wykresie, tzn. wyróżnić je spośród pozostałych danych. Do efektu jak poniżej można dojść w kilku prostych krokach.
Przede wszystkim, żeby dojść do takiej postaci, musimy za pomocą funkcji MAX i MIN określić, które wartości z naszej tabeli są właśnie maksymami, a które minimami. Zrobić to za pomocą formuł z dwóch przyczyn – pierwsza to taka, że będzie zwyczajnie szybciej (w przykładzie mamy tylko kilka wierszy danych, w praktyce może być dużo więcej), a drugi, że w razie zaktualizowania danych, ulec zmianie może również wartość maksymalna lub minimalna.
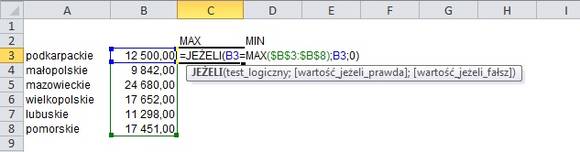
Chcąc użyć tych informacji celem pokazania ich na wykresie, musimy sprawdzić każdą wartość, określając czy jest maksymalną lub minimalną z zakresu. W tym celu użyjemy funkcji JEŻELI. Przypomnę, że funkcja JEŻELI sprawdza test logiczny, u nas będzie nim:
Wartość województwa = wartość maksymalna z całego zakresu
co w przełożeniu na zapis formuły widnieje u nas dla pierwszej komórki jako:
B3=MAX($B$3:$B$8)
Odwołania bezwzględnego (symbol „$”) używamy celem usztywnienia zakresu dla formuły MAX, jest on w końcu ten sam dla wszystkich wartości.
JEŻELI PRAWDA – wówczas chcemy, by w wynikiem była wartość przypisana danemu województwu;
JEŻELI FAŁSZ – u nas będzie to zero; nie chcemy bowiem wyróżniać tego województwa.
Przeciągamy formułę do dołu, to samo robimy dla kolumny MIN – tyle, że zamiast formuły MAX damy MIN. Ok, jestem kapitanem oczywistym.
Mając tak sporządzane dane, tworzymy wykres kolumnowy, wybierając jako zakres całą tabelę.
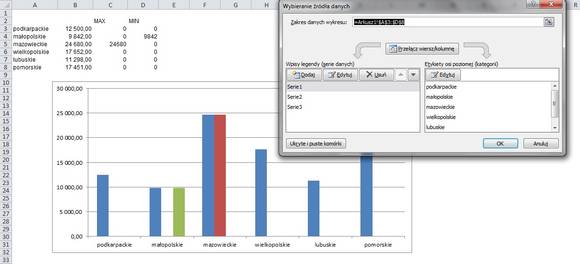
Na razie wykres nie wygląda zbyt sensownie – kolumny z wartościami przypisanymi województwom i z formułami wartości maksymalnych i minimalnych tworzą trzy serie danych, tj. teoretycznie występują one na wykresie tuż obok siebie. W praktyce tego nie widać, gdyż jednemu województwu przypisane są co najwyżej dwie wartości. Teraz wystarczy jednak tylko „nałożyć” na siebie wszystkie serie przypisane poszczególnym wykresom.
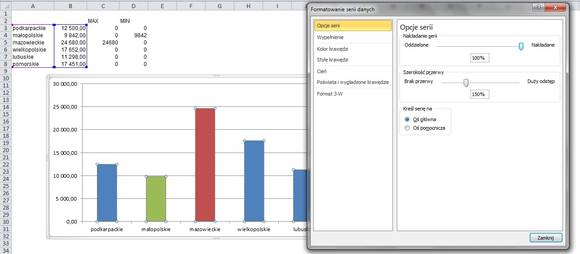
Prawym klawiszem myszki klikamy na dowolnej kolumnie, a następnie:
Formatuj serię danych -> Opcje serii -> Nakładanie serii
Wartość z 0% zmieniamy na 100%. Odtąd kolumny będą się nakładać, a widoczna będzie ta wysunięta najbardziej na prawo w tabeli.
#63 Najczęściej występująca wartość tekstowa
Porada 61 zawierała szereg stosunkowo podstawowych formuł. Za ich pomocą nie da się jednak wprost uzyskać wyniku na następujące pytanie – jaka jest najczęściej występująca wartość tekstowa? Dla nas przykładem będzie poniższy szereg danych z imionami studentów, jak i uzyskanymi przez nich ocenami. Chcemy sprawdzić, jakie jest najczęściej występujące imię. W tym celu użyjemy kombinacji kilku funkcji: PODAJ.POZYCJĘ, INDEKS, MAX i LICZ.JEŻELI. Będzie to porada nieco bardziej zaawansowana.
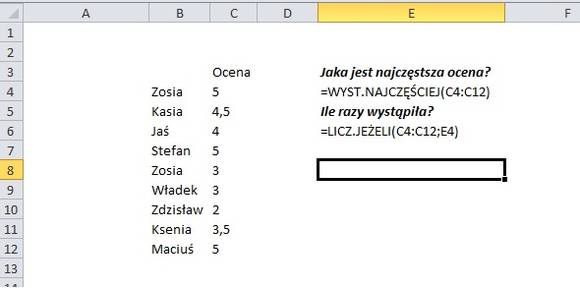
Stosunkowo łatwo i szybko można odpowiedzieć sobie na pytania: jaka ocena występuje najczęściej? (formuła WYST.NAJCZĘŚCIEJ) i ile razy ona wystąpiła? (formuła LICZ.JEŻELI). Nasze pytanie jest jednak nieco bardziej skomplikowane dla Excela. Standardowe formuły poskutkują błędem pracując na formacie tekstowym.
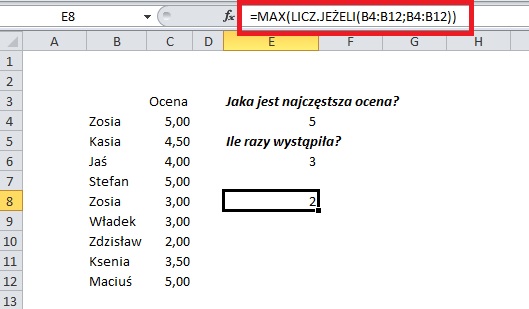
Zacznijmy od funkcji MAX, dla której zakresem danych będzie funkcja LICZ.JEŻELI. W rezultacie otrzymamy ilość powtarzającej się wartości maksymalnej. U nas będzie to liczba 2 – bo i w zestawieniu imię „ZOSIA” występuje dwa razy.
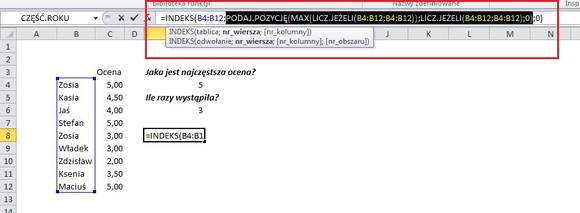
Mając tę informację, chcemy przypisać najczęściej występującej pozycji jej tekstowy odpowiednik. Najpierw musimy jednak wskazać Excelowi, na której pozycji w tabeli znajduje się najczęściej występująca wartość. W tym celu posłużymy się funkcją PODAJ.POZYCJĘ.
Szukaną wartością będzie nasza dotychczasowa funkcja (bo jej wynik jest 2, a zatem wyszukuje odpowiednią ilość wartości maksymalnej). Przeszukiwaną pozycją będzie kolejna funkcja LICZ.JEŻELI z jej niezmienionym zakresem. W rezultacie otrzymamy numer pozycji w naszym zakresie, pod którym występuje imię ZOSIA. Funkcję zatwierdzamy korzystając ze skrótu CTRL + SHIFT + ENTER (gdyż jest to formuła tablicowa).
Widzimy już, że ZOSIA występuje na pozycji 1. Teraz wystarczy już tylko całość poprzedzić formułą INDEKS, która określi jaka wartość (tekstowa) występuje pod podaną pozycją. Jako tabelę zaznaczymy przeszukiwany obszar, numerem wiersza będzie dotychczasowa formuła, a numerem kolumny – 0. Pamiętajmy o skrócie CTRL + SHIFT + ENTER, którym zatwierdzamy formułę.
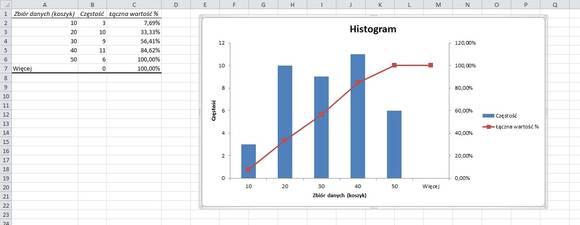
#64 Robimy histogram
Mamy wyniki egzaminu studentów – chcemy sprawdzić jak wygląda nie tylko zdawalność (mak. liczba punktów to 50, zdawalność od 30), ale i generalnie jak wygląda rozkład punktów w poszczególnych przedziałach. Patrząc na dane, ciężko jest cokolwiek wywnioskować. Bardzo dobrą formą wizualizacji tego typu zbiorów jest histogram.
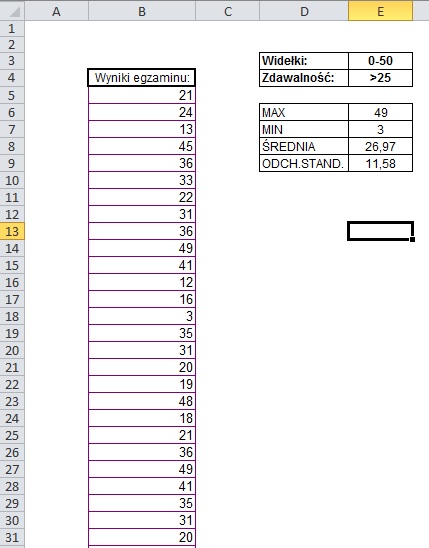Na zrzucie wdarł się mały błąd – założyliśmy, że egzamin traktujemy jako zdany od 30 pkt, do czego dostosowane zostały również przedziały punktowe w dalszej części
Histogram to swego rodzaju wykres, który pokazuje dane agregowanego w zbiorach. Dla nas takimi zbiorami będą poszczególne przedziały punktowe – np. do 10, do 20, do 30, do 40 i do 50.
Standardowo Excel nie posiada możliwości rysowania histogramów. Należy zaopatrzyć program w dodatek Analiza danych. Jeżeli do tej pory tego nie zrobiliście, to można to szybko zmienić. Wystarczy wejść w ustawienia Excela.
Plik -> Opcje -> Dodatki
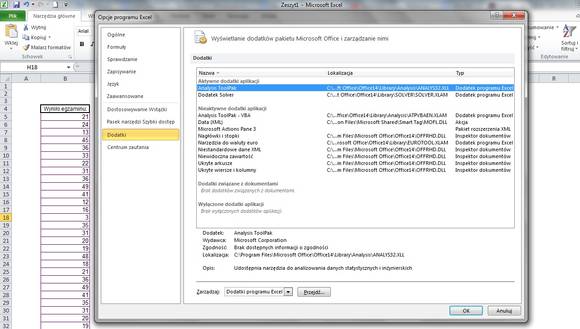
Z listy należy wybrać Analysis Toolpak. Do możliwości tego dodatku dostaniemy się z formatki Dane.
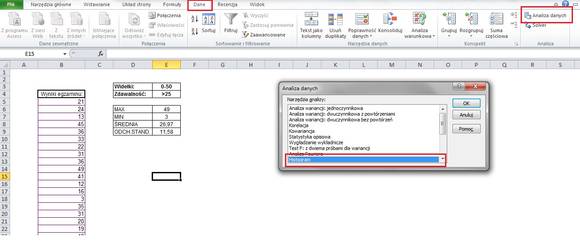
W opcjach histogramu wybieramy kolejno:
– Zakres komórek – u nas to tabela z punktami studentów;
– Zakres zbioru – to nowa tabela, w której zawarliśmy przedziały, które interesują nas w analizie.
Zaznaczamy również opcję Wykres wyjściowy i Łączny udział procentowy. Po kliknięciu OK, wykres pojawi się w nowym arkuszu z naniesionymi parametrami:
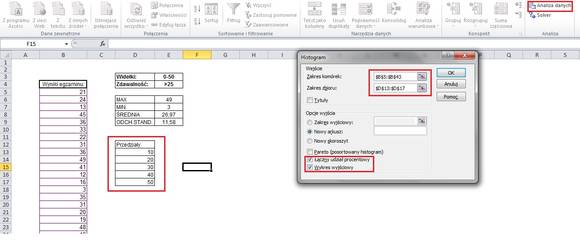
Jest to moim zdaniem bardzo czytelna forma analizowania danych.
#65 Analiza danych – statystyka opisowa
Mamy dane odnośnie sprzedaży dwóch handlowców. Jedną z możliwości szybkiej analizy tych danych, pomijając niezastąpione „na oko”, jest Statystyka opisowa, która skrywa się w opcjach dodatku Analiza danych. Wejdźmy zatem ponownie do tej zakładki, tym razem wybierając: Statystyka opisowa.
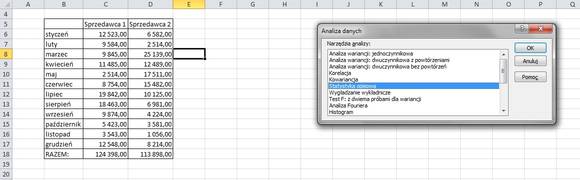
W nowym okienku należy wybrać zakres danych, jak i rodzaj przygotowanego raportu.Proponuję, na początku, wybrać opcję Statystyki podsumowujące. Pojawią się one w następnym arkuszu.
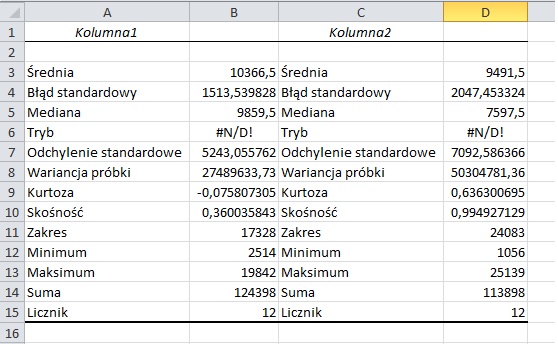
W nowym okienku mamy już wyłożone na tacy najbardziej podstawowe miary statystyczne, które już dają nieco lepszy pogląd na kształtowanie się osiągnięć handlowców. Widzimy chociażby, że w przypadku pierwszego nie tylko średnia i mediana są wyższe, ale i mniejsze jest odchylenie standardowe, stąd można oczekiwać, że jego sprzedaż z miesiąca na miesiąc nie będzie drastycznie się różnić. Mamy też podane minimum, maksimum sprzedaży, jak i wynikający z tych dwóch wartości zakres.
#break#
FORMUŁY FINANSOWE
#66 Szybkie porównywanie lokat – czyli efektywna stopa procentowa
W środowisku formuł finansowych prawdopodobnie najbardziej elementarnymi, a zarazem często wykorzystywanymi przez użytkowników, są formuły poświęcone prostemu obliczeniu efektywnej stopy procentowej. Efektywna stopa mówi nam o tym, jaką faktycznie stopę zwrotu uzyskujemy z danej inwestycji – lokaty, zważywszy na kapitalizację. Weźmy sobie za przykład właśnie lokatę.
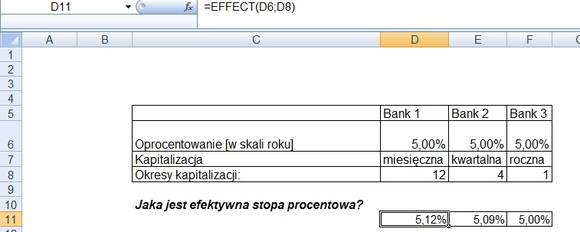
Nasze oszczędności wynoszą 10 tys. zł. Pierwszym krokiem na drodze skutecznego ich ulokowania, będzie wybranie banku oferującego najlepsze oprocentowanie. Mamy w naszym przykładzie trzy warianty, z tym samym oprocentowaniem, ale różnymi okresami kapitalizacji.
Kapitalizacja to inaczej naliczanie odsetek. Jej częstotliwość oznacza więc, jak często do naszego rachunku dopisywane są odsetki. Gdy mamy do czynienia z kapitalizacją miesięczną, wówczas co miesiąc nasz kapitał powiększa się o dodatkowe środki. W kolejnym miesiącu oprocentowanie jest liczone od naszego kapitału powiększonego o dotychczasowe, narastające odsetki. Teoretycznie więc, najwyższe efektywne oprocentowanie, będzie tam, gdzie najczęstsze są kapitalizacje (w przypadku jednakowego oprocentowania). Aby się o tym przekonać, wystarczy zastosować formułę =EFEKTYWNA, dla której argumentami są: oprocentowanie oraz okresy kapitalizacji.
Wyniki są następujące:
#67 Zysk z lokaty
Wydawać by się mogło, że obliczenie zysku z lokaty to sprawa intuicyjna, nie przysparzająca żadnych kłopotów. Czy na pewno?
Do obliczenia realnych zysków z lokaty wykorzystamy jedną z podstawowych formuł finansowych – Future Value, tj. FV. W tym przykładzie założymy, że kapitalizacja jest miesięczna, a oprocentowanie jest skali roku. Później ten przykład będziemy nieco modyfikować.
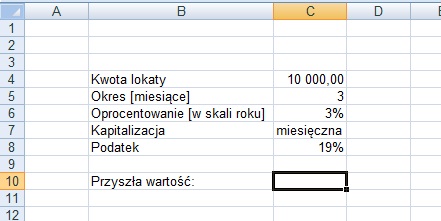
Zacznijmy od prostego kalkulatora, w którym będziemy mogli operować dwiema zmiennymi: oprocentowaniem i okresem przechowywania środków.
Mając wypisane dane jak powyżej, zastosujmy formułę FV, której składnikami są:
Stopa – stopa procentowa dla okresu. U nas 3%, podzielone przez liczbę okresów kapitalizacji (czyli 12).
Liczba_okresów – całkowita liczba okresów płatności w okresie spłaty. U nas są to trzy miesiące. Wiemy, że kapitalizacja następuje co miesiąc, a nasza lokata trwa trzy miesiące.
Rata – płatność dokonywana w każdym okresie; nie może się zmienić w czasie trwania kredytu. U nas wyniesie ona 0, gdyż niczego nie dopłacamy do lokaty.
Wb – wartość bieżąca lub skumulowana wartość przyszłego strumienia płatności według wyceny na dzień obecny. Jeśli argument „wb” zostanie pominięty, przyjmuje się, że ma wartość 0 (zero) i należy określić argument „rata”. Kapitał należy w formule wpisać ze znakiem „-„.
Typ – Argument opcjonalny. Liczba 0 albo 1. Określa, kiedy płatność jest należna. Jeśli zostanie pominięty, przyjmowana jest wartość 0.
Ostatecznie uzyskujemy taki wynik:
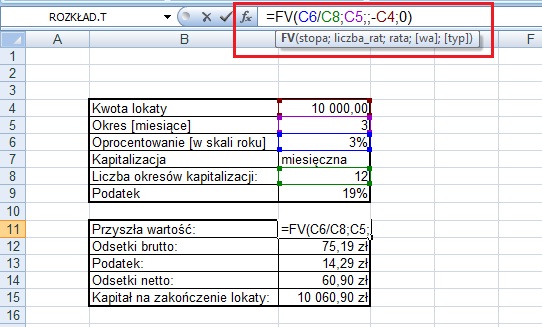
#68 Tworzymy uniwersalny kalkulator lokat
Powyższa wskazówka jest o tyle przydatna, że z pewnością jest najbardziej uniwersalnym rozwiązaniem służącym wyliczaniu odsetek od lokat. Co jednak, gdy mamy do czynienia z inną kapitalizacją lub gdy chcemy porównać różne opcje?
Pozwolę sobie zaznaczyć, że ta wskazówka należy do nieco bardziej zaawansowanych. Ostatecznie musimy uzyskać widok jak poniżej. Na niebieskim tle są pozycje, które będziemy każdorazowo definiować określając parametry lokaty. Okres to liczba miesięcy trwania lokaty. Następnie mamy oprocentowanie oraz kapitalizację. Kapitalizacja stanowi listę rozwijaną w komórce C7 (jak zrobić taką listę opisywałem w pierwszym artykule z cyklu). Jej źródłem są dane w kolumnie F. Zakładamy, że kapitalizacje mogą być tygodniowe, miesięczne, kwartalne i roczne. Z rozwijanej listy będziemy definiować tę wartość określając warunki lokaty.
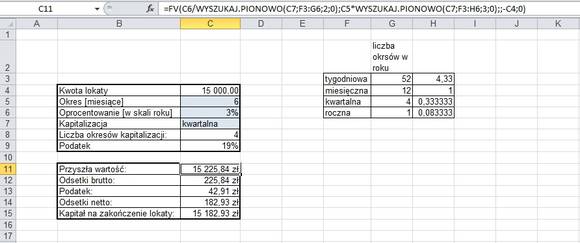
Teraz przechodzimy już do pisania formuły FV. To będzie nasza podstawowa formuła, dlatego rozbiję ją na części składowe dla lepszej czytelności:
– stopa – jest to stopa procentowa, podzielona przez liczbę okresów kapitalizacji. W przypadku miesięcznej kapitalizacji jest to 12 okresów (3%/12), w przypadku kwartalnej – 4 (3%/4). Korzystając z funkcji WYSZUKAJ.PIONOWO, wyszukujemy ilość okresów, odpowiadających częstotliwości kapitalizacji, zdefiniowanych w tabeli obok. 3% będzie więc dzielone przez 12, gdy kapitalizacja jest miesięczna, przez 4, gdy będzie kwartalna, itd.
– liczba_rat – teraz musimy określić, ile razy w ciągu roku następnie kapitalizacja (w ciągu roku, bo zakładamy stopę oprocentowania wyrażoną w skali roku). Dla miesięcznej kapitalizacji, przykładowe 6 miesięcy będzie 6 razy kapitalizowane. Ale gdy kapitalizacja będzie kwartalna, wówczas będą tylko dwie kapitalizacje. Szóstkę będziemy zatem musimy przemnożyć przez wartość 0,333 (1/3). Te informacje zawarliśmy w kolumnie H na zrzucie ekranu. Excel wyszukuje je w punkcie liczba_rat korzystając z funkcji WYSZUKAJ.PIONOWO. W zależności od rodzaju kapitalizacji, ilość miesięcy jest mnożona przez odpowiedni współczynnik.
– parametr wa/wb (w zależności od wersji Office’a) – to po prostu wskazanie komórki z kapitałem, tyle że z minusem. Minus możemy też postawić przed całą formułą.
W ten sposób uzyskujemy uniwersalny kalkulator, w którym możemy zmieniać okresy kapitalizacji, oprocentowanie, wielkość kapitału. Pozwala to na łatwe i szybkie obliczanie odsetek od lokaty i porównywanie różnych ofert.
#69 Co miesiąc odkładam określoną kwotę. Ile uzbieram w okresie X, na oprocentowanym rachunku?
Korzystacie z pakietów systematycznego oszczędzenia? Lub – być może – sami opracowaliście system stałych przelewów na konto oszczędnościowe? Jeżeli tak, to być może interesuje Was, ile uzbieracie po określonej liczbie miesięcy lub lat. Procent składany jest wówczas waszym sprzymierzeńcem.
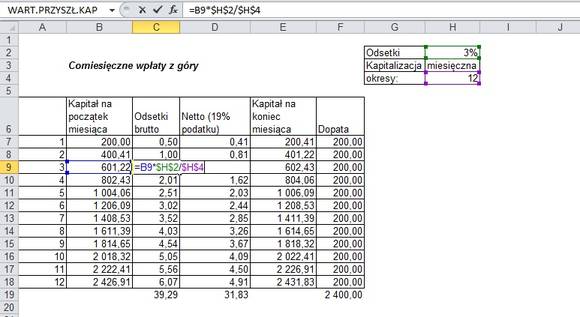
Ja w takich sytuacjach preferuję korzystanie z prostej tabeli. Zakładając, że wpłaty mają miejsce na początku miesiąca (z góry), co miesiąc dopłacamy po 200 zł, a oprocentowanie wynosi 3% w skali roku, możemy łatwo skonstruować przebieg kształtowania się kapitału. Zaczynamy od kapitału 200 zł. Następnie liczymy od niego odsetki, mnożąc przez 3%/12, a następnie odejmując podatek (odsetki*0,81). Odsetki + kapitał z początku miesiąca, daje kapitał na koniec miesiąca i początek następnego, itd.
Zastosowanie tabeli jest o tyle dobrym pomysłem, że w razie zmiany oprocentowania, można łatwo je zastąpić w tabeli – aplikując nową wartość do późniejszych wpłat. Jest ona również korzystna przy zmianie wysokości miesięcznych wpłat.
#70 Podwojenie kapitału – jak szybko je policzyć?
Ten ekspresowy life-hack nie jest szczególnie związany z Excelem, ale już na pewno z omawianą w tej części artykułu tematyką. Aby szybko policzyć, po ilu latach podwoi się nasz kapitał, przy danym oprocentowaniu, wystarczy zastosować Regułę 72. 72 dzielimy przez oprocentowaniu i wychodzi nam wynik w latach, przy założeniu oprocentowania składanego. Tak więc przy 8%, kapitał podwoi się po 9 latach. Sprawdźcie sami 😉
#71 Chcę uzbierać kwotę X, przy oprocentowaniu Y, w ciągu Z lat. Ile muszę odkładać co miesiąc? Jaki wpływ ma inflacja?
Jest to dosyć powszechny dylemat w finansach osobistych. Mając w pamięci jakiś projekt, zadanie, które musimy sfinansować w przyszłości (np. zakup samochodu albo zorganizowanie wesela), zastanawiamy się, ile pieniędzy powinniśmy oszczędzać, chcąc regularnie odkładać, by dojść do danej kwoty, wykorzystując przy tym również narastające odsetki. Zakładamy więc, że jest to stosunkowo odległe zadanie (np. mieszkanie dla dziecka, które obecnie ma 2 latka).
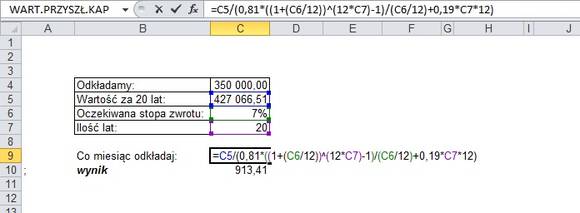
Załóżmy, że współcześnie takie mieszkania kosztują ok. 350 tys. zł. Mając w perspektywie długoterminowe oszczędzanie (ok. 20 lat), należy wziąć pod uwagę ew. wzrost cen wynikający z inflacji. Ceny mieszkań nie zachowują się co prawda idealnie na wzór trendu inflacji, jednakże – dla uproszczenia – jakąś stopę przyrostu cen wypadałoby do obliczeń przyjąć. Załóżmy więc, że ceny średniorocznie będą rosły o 1%, a zatem musimy naszą wyjściową kwotę uaktualnić do tej wartości.
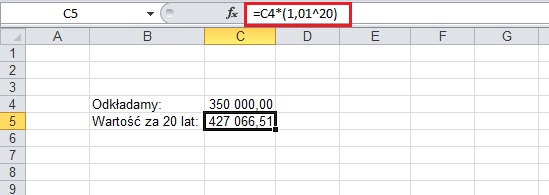
Takiej operacji dokonamy stosując wzór na procent składany. Kapitał bieżący należy przemnożyć razy 1,01 podniesione do potęgi odpowiadającej ilości lat (u nas 20).
Wiemy już, że powinniśmy odłożyć ponad 427 tys. zł. Ile w takim razie powinniśmy odkładać co miesiąc, by uzyskać tę kwotę? Nie wystarczy podzielić kapitału przez ilość miesięcy. Należy w końcu mieć na uwadze, że środki będą na siebie pracowały, osiągając określoną stopę zwrotu. Załóżmy, że środki będą inwestowane i stopa zwrotu przewyższy oprocentowanie lokat i wyniesie 7% rocznie.
Formuła służąca do takich wyliczeń będzie – powiedzmy – umiarkowanie skomplikowana, wynikająca z wprost z matematyki finansowej. Kwotę kapitału sprowadzonego do wartości przyszłej (nasze 427 tys.) dzielimy przez oprocentowanie w skali miesiące podniesione do potęgi odpowiadającej ilości miesięcy, uwzględniając przy tym opodatkowanie.
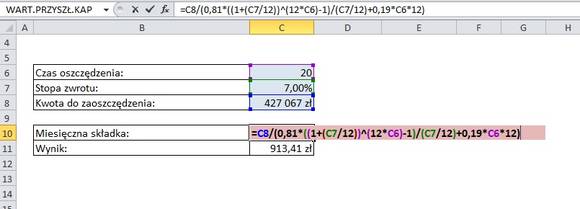
O wiele szybciej i prościej można by to policzyć stosując formułę PMT, jednakże ona nie uwzględnia opodatkowania.
#72 Ile kosztuje kredyt?
Excel znajduje również zastosowanie na etapie poszukiwania odpowiedniego kredytu. Co jednak ważne, daje on realny pogląd na to, ile kredyt w rzeczywistości kosztuje – jaka część spłacanej raty to odsetki, a jaka to kapitał.
W przypadku kredytów nie będzie interesowała nas przyszła wartość pieniądza, a właśnie rata kredytu. Użyjemy więc innej formuły – PMT. Przedstawmy sobie jej komponenty:
PMT (stopa;liczba_rat;wartość_bieżąca; wartość_przyszła; typ )
STOPA – stopa procentowa dla okresu. Na przykład w przypadku pożyczki na samochód oprocentowanej na 10 procent rocznie ze spłatami miesięcznymi miesięczna stopa procentowa to 10 procent podzielone przez 12, czyli 0,83 procent. Dlatego jako argument stopa należy wprowadzić w formule wartość 10%/12 albo 0,83% lub 0,0083.
LICZBA_RAT – całkowita liczba okresów płatności w okresie spłaty. Na przykład osoba otrzymująca czteroletnią pożyczkę na samochód, spłacająca tę pożyczkę w miesięcznych ratach, będzie ją spłacać przez 4*12 (czyli 48) okresów. Dlatego jako argument liczba_rat należy wprowadzić w formule liczbę 48.
WARTOŚĆ_BIEŻĄCA, czyli aktualna łączna wartość serii przyszłych płatności (nazywana także kapitałem). U nas będzie to kwota zaciągniętego kredytu.
WARTOŚĆ_PRZYSZŁA – wartość przyszła lub saldo gotówkowe, do którego zmierza się po dokonaniu ostatniej płatności. Z tego argumentu korzystamy zamiast powyższego, chcąc obliczyć miesięczną kwotę oszczędności.
TYP – mówi nam o tym, kiedy płatność jest należna (1 – koniec miesiąca, 0 – początek).
Zakładając więc, że – jak na zdjęciu poniżej – chcemy zaciągnąć kredyt na 25 tys. zł, przy oprocentowaniu wynoszącym 6% w skali roku, na okres 3 lat, możemy łatwo policzyć naszą ratę kredytu:
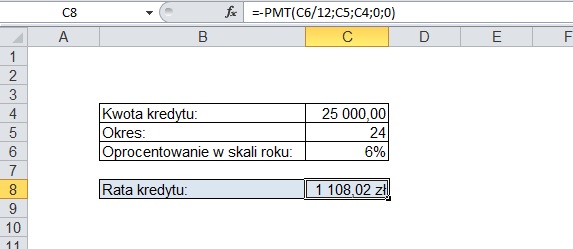
Nasza rata wynosi 1108,02 zł. Wiedząc to, możemy łatwo sprawdzić, czy oprocentowanie proponowane przez pożyczkodawcę jest faktycznie takie, jak twierdzi, czy też może w umowę zostały wkomponowane jakieś dodatkowe opcje.
#73 Tworzymy harmonogram spłat
Obliczenia doradcy kredytowego można skonfrontować przy użyciu własnoręcznie policzonego harmonogramu spłaty kredytu. Uwaga, w tym przypadku cały czas zakładamy, że mamy do czynienia ze stałym oprocentowaniem i tak zwanymi równymi ratami.
Zacznijmy od utworzenia tabeli, w której uzupełnimy potrzebne rubryki. Tabela posiadać będzie 24 wiersze, bo tyle jest okresów (plus dodatkowy na nagłówki i drugi na sumy), w jednej kolumnie określać będziemy ratę kredytu (policzyliśmy ją w poprzednim punkcie), a następnie, przy użyciu nowej formuły, rozbijemy ją na część kapitałową i odsetkową.
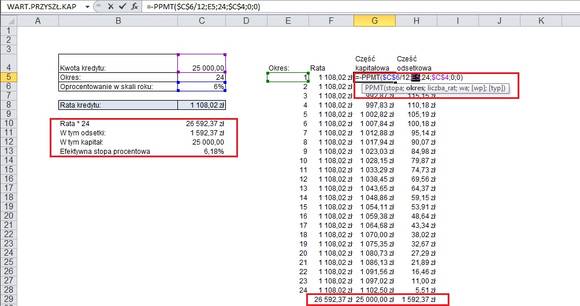
Formuła działa analogicznie do poprzedniej. Stopa procentowa to stopa roczna, podzielona na ilość okresów (u nas 12), okres to numer danego miesiąca, dla którego dokonywane są obliczenia. Liczba rat to ilość miesięcy, a kapitał początkowy to kwota zaciągniętego kredytu.
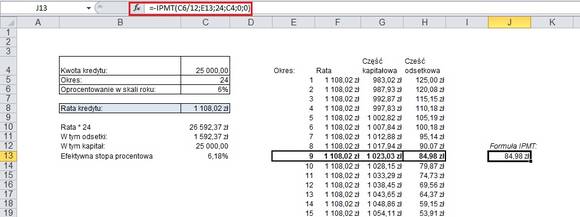
#74 Ile odsetek jest w jednej racie?
Ta porada będzie krótka, ale być może przydatna. Funkcja IPMT oblicza ile w danej płatności jest odsetek. Argumentami dla niej są: stopa procentowa (na wzór dotychczasowych – tj. stopa podzielona przez ilość kapitalizacji), okres dotyczy wybranego miesiąca, dla którego chcemy uzyskać kwotę odsetek.
#75 Tabela danych z dwiema zmiennymi – różne oprocentowania i czas trwania kredytu
Teraz wykorzystajmy trick, który omówiliśmy sobie w jednym z poprzednich artykułów – tabelę danych. Przypomnę, że przedstawia ona wyniki różnych kombinacji wykorzystywanych w równaniu. My ustalamy, że bierzemy kredyt na 100 tys. zł, ale chcemy sprawdzić, ile wynosić będzie rata przy różnym poziomie oprocentowania i różnym okresie spłaty. Jak to zrobić?
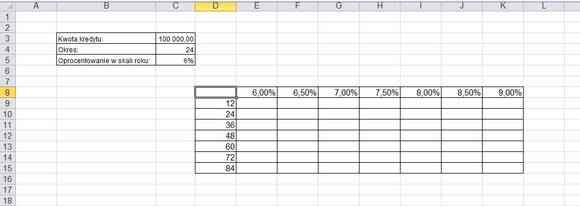
Przygotowałem – na razie jeszcze pustą – tabelę. W wierszu mamy poziom oprocentowania, w kolumnie – czas trwania kredytu (okresem jest dla nas miesiąc).
W rogu tabeli, jak na poniższym zdjęciu, wpisujemy formułę PMT, uwzględniając dane z wyjściowej tabeli. Następnie, po zaznaczeniu całej tabeli, którą chcemy uzupełnić wynikami różnych zmiennych tej formuły, klikamy na formatkę Dane -> Analiza warunkowa -> Tabela danych. Argumentem dla wierszy będzie u nas oprocentowanie (komórka C5 podzielona przez 12), a dla okresu C4. Tabel danych wykorzystywać będzie następnie różne kombinacje tych zmiennych, zdefiniowane w wierszach i kolumnach.
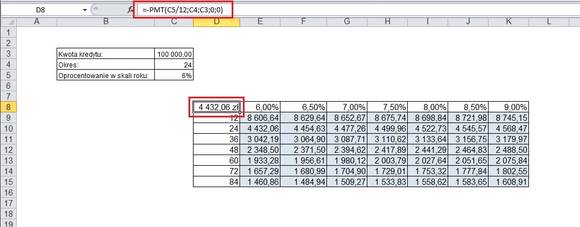
Na podobnej zasadzie można stworzyć tabelę danych dla lokat.
#76 Raty malejące
Pokrótce – celem dopełniania tematyki kredytów – przedstawimy sobie tabelę, w której można obliczać oprocentowanie kredytu w systemie rat malejących. Zasadniczo model ten polega na tym, że co miesiąc spłacamy tę samą, równą wartość zaciągniętego kapitału, a odsetki naliczane są od kapitału, który pozostaje do spłaty. Raty malejące wywodzą swą nazwę od tego, że z okresu na okres spada część odsetkowa.
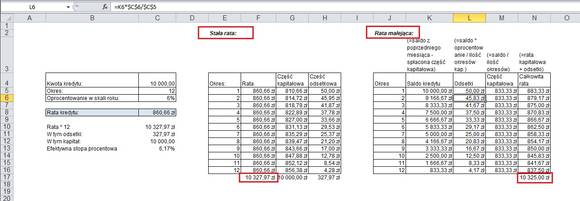
Sposób obliczenia przedstawiłem na poniższym zdjęciu – mam nadzieję, że okaże się to dla Was wystarczająco czytelne. Pamiętajcie, że odsetki naliczają się od kapitału pozostałego na początek miesiąca. W rubryce K odejmujemy zatem od kapitału z zeszłego miesiąca, część raty kapitałowej. Odsetki obliczane są od tej wartości (jest to iloczyn salda na początek miesiąca i oprocentowania podzielonego przez ilość okresów odsetkowych).
#77 Jak obliczyć roczną stopę zwrotu z inwestycji?
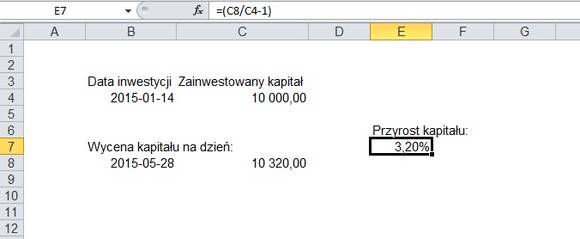
No właśnie – powiedzmy, że w styczniu zainwestowaliście kapitał, którego przyrost [(kapitał końcowy/kapitał początkowy -1 )*100%] wyniósł ok. 3%. Czy to dużo? Porównujecie zapewne ten wynik do lokaty, która daje mniej więcej tyle samo, tyle że bez ryzyka i… w skali roku. Jak sprawić, by tę stopę zwrotu sprowadzić do tej samej skali? Służy temu metodą rocznej stopy zwrotu CAGR, funkcjonująca w Excelu pod formułą XIRR.
Celem wykorzystania formuły XIRR, musimy nieco zmienić wygląd naszej tabeli, gdyż formuła jest dość wymagająca jeżeli chodzi właśnie o układ danych, jak i ich zapis.
W pierwszej kolumnie możemy napisać komentarz. U nas jest to po prostu „Data inwestycji”, aczkolwiek zaleca się, by był on bardziej szczegółowy, jak „Zakup jednostek funduszy inwestycyjnego XYZ”. W drugiej kolumnie piszemy datę dokonania tejże operacji. W trzeciej natomiast – określamy wpłatę lub wypłatę kapitały. Wpłata jest – na przekór – ze znakiem minus, ponieważ niejako „wychodzi” ona z naszego konta, na rzecz dokonania inwestycji/lokaty. A zatem nasze 10 tys. wpisujemy ze znakiem minus.
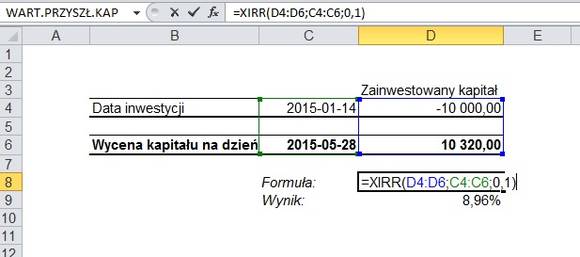
U dołu dokonujemy wyceny kapitału. Komentarz to „Wycena”, a data jest bieżąca (skrót CTRL + ;), tak byśmy mogli codziennie znać faktycznie osiąganą stopę zwrotu (jeżeli wartość inwestycji się nie zmieni, to stopa procentowa będzie z dnia na dzień spadać w skali roku!). Wartość wyceny traktujemy jako wpływ, czyli określamy ją bez minusa.
Formuła XIRR ma następujące argumenty:
wartość;data;wynik.
Nasza wartość to zakres uwzględniający zainwestowany kapitał (otwiera on zakres) i jego wycena (zamknięcie zakresu). Różnica w wycenie zostanie odniesiona do zainwestowanego kapitału i daty dokonania inwestycji. Data również stanowi zbiór rozpoczynający się w dniu dokonania inwestycji, zamykając na dniu wyceny. Wynik jest argumentem opcjonalnym.
Jak więc widzicie, nasze 3.2%, to blisko 9% w skali roku.
#78 Amortyzacja – Excel zna wiele metod liczenia
Nad tą wskazówką nie będę się szczególnie rozwodził. Uznałem jednak, że warto ją przytoczyć ze względu na małych przedsiębiorców, którzy zapewne nie korzystają z wyrafinowanych programów finansowo-księgowych, prowadząc księgowość na własną rękę. Amortyzacja w Excelu może być liczona według pięciu formuł:
SLN – metoda liniowa, wynik podany w skali roku. Excel podpowiada, by do jej wyliczenia uwzględnić tzw. wartość odzyskiwalną.
DB i DDB – metody degresywne, wykorzystujące stałe, współczynniki.
SYD – metoda sumy cyfr wszystkich lat amortyzacji
VDB – metoda podwójnie malejącego salda. Jest to też formuła, która potrafi na stosunkowo najbardziej zróżnicowanie określenie parametrów amortyzacji.
#79 Konwersja jednostek
Problem konwersji jednostek matematycznych, fizycznych lub innych, jest dość typowy. Zapewne każdy z Was wypracował już jakieś rozwiązanie dla tego typu zadania, ale pracując już w Excelu, można spokojnie dokonać odpowiednich obliczeń przy użyciu jednej formuły. Chodzi o formułę KONWERTUJ, która składa się zasadniczo z trzech argumentów: konwertowanej wartości, jej dotychczasowej jednostki, jednostki docelowej. Nazwę jednostki określamy stosownym skrótem – cm, kg, mil, lbm, m3, itp. Pełną listę skrótów i obsługiwanych wielkości znajdziemy pod linkiem:https://support.office.com/pl-pl/article/KONWERTUJ-funkcja-d785bef1-808e-4aac-bdcd-666c810f9af2 Konwersje wartości zapisanych w systemach dwójkowym, ósemkowym, dziesiętnym i szesnastkowym dokonuje się poprzez dedykowane formuły, rozpoczynające się od nazwy systemu który konwertujemy.
#80 Zaokrąglenia
Dla Excela nic nie jest oczywiste i na każde zadanie znajduje on wiele rozwiązań – naprawdę wszystko jest przemyślane. Nawet tak – pozornie – prosta operacja jak zaokrąglanie wartości, może być przeprowadzona przy użyciu kilku formuł.
ZAOKR – zaokrągla uwzględniając ilość miejsc po przecinku
ZAOKR.DO.PARZ / ZAOKR.NPARZ / ZAOKR.DO.CAŁK – do najbliższych parzystych, nieparzystych, całkowitych
ZAOKR.W.GÓRĘ / ZAOKR.W.DÓŁ – przydatne zwłaszcza przy dokonywaniu obliczeń finansowych – banki i urzędy skarbowe zazwyczaj zaokrąglają na niekorzyść klienta/podatnika
ZAOKR.DO.WIELOKR – zaokrągla do najbliższej wielokrotności wskazanej liczby. (ZAOKR.DO.WIELOKR(11,23;5) zostanie zaokrąglone do wielokrotności piątki, czyli w tym przykładzie do 10.
ZAOKR.DO.TEKST – zaokrągla, zmieniając format komórki na tekstowy
LICZB.CAŁK – sprowadza liczbę do wartości całkowitej bez zaokrąglania (8,9 będzie zapisane jako 8).
To by było na tyle jeżeli chodzi o czwarty artykuł z cyklu poświęconego programowi Excel. Przed nami jeszcze jedna odsłona. W niej przejdziemy sobie przez tabele przestawne, a także inne, nieprzypisane do tematyki poszczególnych odsłon lub – nie oszukując – pominięte tricki, które przyszły mi do głowy w trakcie pisania cyklu. W tym misz-miszu będzie więc mowa o zabezpieczaniu danych, komórek, arkuszy, pobieraniu aktualizujących się danych z internetu i jeszcze wielu innych, przydatnych rzeczach. W piątym artykule będziecie mogli też pobrać ściągawkę z przydatnymi skrótami!
